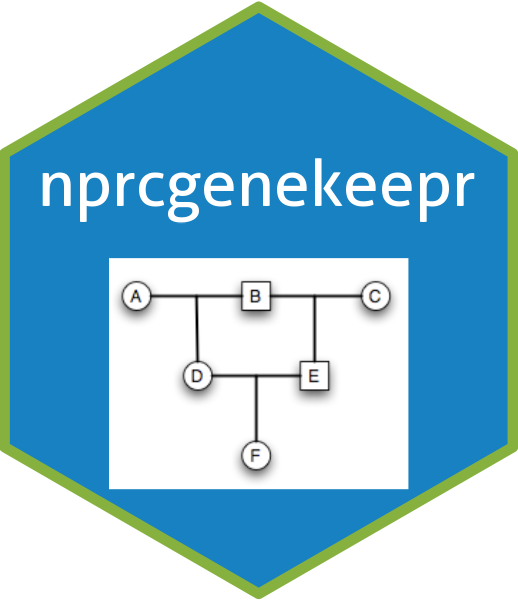
Quick Example of Simulated Kinships with Partial Parentage

Introduction

This vignette provides a quick example of how to estimate kinship coefficients using simulation. One simulation uses 100 iterations and the other uses the same setup with 1000 simulations to illustrate the type of kinship coefficient estimate variance you can expect with a simple pedigree exhibiting partial parentage for some of the members.

Anticipation of further uses of this kinship estimation method

Retention of founder alleles is a primary driving force behind this package of utilities. This example is intentionally overly simplistic to clearly illustrate this one aspect of the methodology used with realistic pedigrees.

In this example, some of the potential parents are not members of the example pedigree and thus, by definition, have a kinship coeficient of 0.0 with all other pedigree members.

In practice most or all of the potential parents will be members of the same pedigree and will potentially have nonzero kinship coeficients with other pedigree members.

Identification of potential parents

This tutorial assumes knowledge of potential parents and does not present methods for identifying potential parents.

Capabilities to be address with resolution of Issue #28¹ will provide users the ability to fully automate the identification of potential parents. However, prior to that capability being available, users can use other methods to identify potential parents.

Creation of example pedigree²

The example is based on the following simple pedigree setup. In the pedigree given below, all of the original animals have identifiers that are single letters of the alphabet.:

Only those IDs that have unknown parents are included in the lists. For those IDs with one known parent, the known parent is included in the . See for ID . Note also that potential parents can either come from the pedigree being augmented by simulation or from outside the pedigree. See , , , and for examples of this.

Currently, if you want to provide differential weights for the different potential parents, you will need to do this directly by modifying the number of times each parent is included in the list.

Animals , , and

knitr::opts_chunk$set(echo = TRUE)
library(kableExtra)
library(magrittr)
library(nprcgenekeepr)
library(stringi)

ped <- nprcgenekeepr::smallPed
simParent_1 <- list(id = "A", # nolint: object_name_linter
                    sires = "Q",
                    dams = c("d1_1", "d1_2", "d1_3", "d1_4"))
simParent_2 <- list(id = "B", # nolint: object_name_linter
                    sires = c("s1_1", "s1_2", "s1_3"),
                    dams = c("d1_1", "d1_2", "d1_3", "d1_4"))
simParent_3 <- list(id = "E", # nolint: object_name_linter
                    sires = c("A", "C", "s1_1"),
                    dams = c("d3_1", "B"))
simParent_4 <- list(id = "J", # nolint: object_name_linter
                    sires = c("A", "C", "s1_1"),
                    dams = c("d3_1", "B"))
simParent_5 <- list(id = "K", # nolint: object_name_linter
                    sires = c("A", "C", "s1_1"),
                    dams = c("d3_1", "d1_2"))
simParent_6 <- list(id = "N", # nolint: object_name_linter
                    sires = c("A", "C", "s1_2"),
                    dams = c("d3_1", "B"))
allSimParents <- list(simParent_1, simParent_2, simParent_3,
                      simParent_4, simParent_5, simParent_6)

extractKinship <- function(simKinships, id1, id2, simulation) {
  ids <- dimnames(simKinships[[simulation]])[[1]]
  simKinships[[simulation]][seq_along(ids)[ids == id1],
                            seq_along(ids)[ids == id2]]
}

extractKValue <- function(kValue, id1, id2, simulation) {
  kValue[kValue$id_1 ==  id1 & kValue$id_2 == id2, paste0("sim_", simulation)]
}

Small Example

This is the simulation. I am only printing out rows with kinship values that vary.

Before running these simulations, take time to look at the included function descriptions to see what they are expecting as arguments and what they return.

?createSimKinships
?kinshipMatricesToKValues
?extractKValue

# Only set this seed if you want to get the same simulation results each time.
set.seed(1)
n <- 10
simKinships <- createSimKinships(ped, allSimParents, pop = ped$id, n = n)
kValues <- kinshipMatricesToKValues(simKinships)
extractKValue(kValues, id1 = "A", id2 = "F", simulation = 1:n)

##  [1] "sim_1"  "sim_2"  "sim_3"  "sim_4"  "sim_5"  "sim_6"  "sim_7"  "sim_8" 
##  [9] "sim_9"  "sim_10"

counts <- countKinshipValues(kValues)
counts$kinshipIds[1:3]

## NULL

counts$kinshipValues[1:3]

## NULL

counts$kinshipCounts[1:3]

## NULL

stats_10 <- summarizeKinshipValues(counts)
nrow(stats_10[stats_10$sd > 0.0, ])

## [1] 94

kable(stats_10[stats_10$sd > 0.0, ], longtable = TRUE) %>%
  kable_styling(latex_options = c("striped", "repeat_header"),
                repeat_header_method = "replace",
                repeat_header_text = "\\textit{(continued)}")

	id_1	id_2	min	secondQuartile	mean	median	thirdQuartile	max	sd
5	A	E	0.00000	0.00000	0.075000	0.000000	0.25000	0.25000	0.1207615
6	A	F	0.12500	0.12500	0.162500	0.125000	0.25000	0.25000	0.0603807
7	A	G	0.12500	0.12500	0.162500	0.125000	0.25000	0.25000	0.0603807
9	A	I	0.25000	0.25000	0.262500	0.250000	0.25000	0.37500	0.0395285
10	A	J	0.00000	0.00000	0.025000	0.000000	0.00000	0.25000	0.0790569
11	A	K	0.00000	0.00000	0.125000	0.125000	0.25000	0.25000	0.1317616
12	A	L	0.12500	0.12500	0.187500	0.187500	0.25000	0.25000	0.0658808
14	A	N	0.00000	0.00000	0.100000	0.000000	0.25000	0.25000	0.1290994
21	B	E	0.00000	0.00000	0.150000	0.250000	0.25000	0.25000	0.1290994
22	B	F	0.12500	0.12500	0.200000	0.250000	0.25000	0.25000	0.0645497
23	B	G	0.12500	0.12500	0.200000	0.250000	0.25000	0.25000	0.0645497
25	B	I	0.00000	0.00000	0.062500	0.062500	0.12500	0.12500	0.0658808
26	B	J	0.00000	0.00000	0.125000	0.125000	0.25000	0.25000	0.1317616
30	B	N	0.00000	0.00000	0.100000	0.000000	0.25000	0.25000	0.1290994
36	C	E	0.00000	0.00000	0.112500	0.125000	0.25000	0.25000	0.1094494
37	C	F	0.12500	0.12500	0.181250	0.187500	0.25000	0.25000	0.0547247
38	C	G	0.12500	0.12500	0.181250	0.187500	0.25000	0.25000	0.0547247
40	C	I	0.12500	0.12500	0.162500	0.156250	0.18750	0.25000	0.0437004
41	C	J	0.00000	0.00000	0.075000	0.062500	0.12500	0.25000	0.0874007
42	C	K	0.00000	0.00000	0.062500	0.062500	0.12500	0.12500	0.0658808
43	C	L	0.25000	0.25000	0.281250	0.281250	0.31250	0.31250	0.0329404
45	C	N	0.00000	0.00000	0.100000	0.125000	0.12500	0.12500	0.0527046
50	D	E	0.00000	0.00000	0.112500	0.125000	0.25000	0.25000	0.1094494
51	D	F	0.25000	0.25000	0.306250	0.312500	0.37500	0.37500	0.0547247
52	D	G	0.25000	0.25000	0.306250	0.312500	0.37500	0.37500	0.0547247
54	D	I	0.12500	0.12500	0.162500	0.156250	0.18750	0.25000	0.0437004
55	D	J	0.00000	0.00000	0.075000	0.062500	0.12500	0.25000	0.0874007
56	D	K	0.00000	0.00000	0.062500	0.062500	0.12500	0.12500	0.0658808
57	D	L	0.12500	0.12500	0.156250	0.156250	0.18750	0.18750	0.0329404
59	D	N	0.00000	0.00000	0.100000	0.125000	0.12500	0.12500	0.0527046
64	E	F	0.25000	0.25000	0.306250	0.312500	0.37500	0.37500	0.0547247
65	E	G	0.25000	0.25000	0.306250	0.312500	0.37500	0.37500	0.0547247
66	E	H	0.00000	0.00000	0.112500	0.125000	0.25000	0.25000	0.1094494
67	E	I	0.00000	0.00000	0.068750	0.031250	0.12500	0.25000	0.0905711
68	E	J	0.00000	0.00000	0.062500	0.000000	0.12500	0.25000	0.0883883
69	E	K	0.00000	0.00000	0.087500	0.125000	0.12500	0.12500	0.0603807
70	E	L	0.00000	0.00000	0.100000	0.093750	0.18750	0.18750	0.0733617
71	E	M	0.00000	0.00000	0.037500	0.000000	0.12500	0.12500	0.0603807
72	E	N	0.00000	0.00000	0.050000	0.000000	0.12500	0.25000	0.0874007
74	E	P	0.00000	0.00000	0.018750	0.000000	0.06250	0.06250	0.0301904
75	E	Q	0.00000	0.00000	0.037500	0.000000	0.12500	0.12500	0.0603807
76	F	F	0.50000	0.50000	0.556250	0.562500	0.62500	0.62500	0.0547247
77	F	G	0.25000	0.25000	0.306250	0.312500	0.37500	0.37500	0.0547247
78	F	H	0.12500	0.12500	0.181250	0.187500	0.25000	0.25000	0.0547247
79	F	I	0.06250	0.06250	0.115625	0.093750	0.12500	0.25000	0.0608283
80	F	J	0.00000	0.00000	0.068750	0.062500	0.12500	0.25000	0.0804177
81	F	K	0.00000	0.00000	0.075000	0.062500	0.12500	0.12500	0.0395285
82	F	L	0.06250	0.06250	0.128125	0.125000	0.18750	0.18750	0.0452856
83	F	M	0.06250	0.06250	0.081250	0.062500	0.12500	0.12500	0.0301904
84	F	N	0.00000	0.00000	0.075000	0.062500	0.12500	0.18750	0.0574335
86	F	P	0.03125	0.03125	0.040625	0.031250	0.06250	0.06250	0.0150952
87	F	Q	0.06250	0.06250	0.081250	0.062500	0.12500	0.12500	0.0301904
88	G	G	0.50000	0.50000	0.556250	0.562500	0.62500	0.62500	0.0547247
89	G	H	0.12500	0.12500	0.181250	0.187500	0.25000	0.25000	0.0547247
90	G	I	0.06250	0.06250	0.115625	0.093750	0.12500	0.25000	0.0608283
91	G	J	0.00000	0.00000	0.068750	0.062500	0.12500	0.25000	0.0804177
92	G	K	0.00000	0.00000	0.075000	0.062500	0.12500	0.12500	0.0395285
93	G	L	0.06250	0.06250	0.128125	0.125000	0.18750	0.18750	0.0452856
94	G	M	0.06250	0.06250	0.081250	0.062500	0.12500	0.12500	0.0301904
95	G	N	0.00000	0.00000	0.075000	0.062500	0.12500	0.18750	0.0574335
97	G	P	0.03125	0.03125	0.040625	0.031250	0.06250	0.06250	0.0150952
98	G	Q	0.06250	0.06250	0.081250	0.062500	0.12500	0.12500	0.0301904
100	H	I	0.12500	0.12500	0.162500	0.156250	0.18750	0.25000	0.0437004
101	H	J	0.00000	0.00000	0.075000	0.062500	0.12500	0.25000	0.0874007
102	H	K	0.00000	0.00000	0.062500	0.062500	0.12500	0.12500	0.0658808
103	H	L	0.12500	0.12500	0.156250	0.156250	0.18750	0.18750	0.0329404
105	H	N	0.00000	0.00000	0.100000	0.125000	0.12500	0.12500	0.0527046
109	I	I	0.50000	0.50000	0.512500	0.500000	0.50000	0.62500	0.0395285
110	I	J	0.25000	0.25000	0.262500	0.250000	0.25000	0.37500	0.0395285
111	I	K	0.00000	0.00000	0.075000	0.093750	0.12500	0.18750	0.0709558
112	I	L	0.06250	0.06250	0.118750	0.125000	0.15625	0.21875	0.0506040
113	I	M	0.12500	0.12500	0.131250	0.125000	0.12500	0.18750	0.0197642
114	I	N	0.00000	0.00000	0.068750	0.062500	0.12500	0.18750	0.0687816
116	I	P	0.06250	0.06250	0.065625	0.062500	0.06250	0.09375	0.0098821
117	I	Q	0.12500	0.12500	0.131250	0.125000	0.12500	0.18750	0.0197642
119	J	K	0.00000	0.00000	0.025000	0.000000	0.00000	0.12500	0.0527046
120	J	L	0.00000	0.00000	0.050000	0.031250	0.06250	0.18750	0.0645497
121	J	M	0.00000	0.00000	0.012500	0.000000	0.00000	0.12500	0.0395285
122	J	N	0.00000	0.00000	0.037500	0.000000	0.12500	0.12500	0.0603807
124	J	P	0.00000	0.00000	0.006250	0.000000	0.00000	0.06250	0.0197642
125	J	Q	0.00000	0.00000	0.012500	0.000000	0.00000	0.12500	0.0395285
127	K	L	0.25000	0.25000	0.281250	0.281250	0.31250	0.31250	0.0329404
128	K	M	0.00000	0.00000	0.062500	0.062500	0.12500	0.12500	0.0658808
129	K	N	0.00000	0.00000	0.050000	0.000000	0.12500	0.12500	0.0645497
131	K	P	0.00000	0.00000	0.031250	0.031250	0.06250	0.06250	0.0329404
132	K	Q	0.00000	0.00000	0.062500	0.062500	0.12500	0.12500	0.0658808
133	L	L	0.50000	0.50000	0.531250	0.531250	0.56250	0.56250	0.0329404
134	L	M	0.06250	0.06250	0.093750	0.093750	0.12500	0.12500	0.0329404
135	L	N	0.00000	0.00000	0.075000	0.062500	0.12500	0.12500	0.0493007
137	L	P	0.03125	0.03125	0.046875	0.046875	0.06250	0.06250	0.0164702
138	L	Q	0.06250	0.06250	0.093750	0.093750	0.12500	0.12500	0.0329404
140	M	N	0.00000	0.00000	0.050000	0.000000	0.12500	0.12500	0.0645497
146	N	P	0.00000	0.00000	0.025000	0.000000	0.06250	0.06250	0.0322749
147	N	Q	0.00000	0.00000	0.050000	0.000000	0.12500	0.12500	0.0645497

A larger simulation

set.seed(1)
n <- 100
simKinships <- createSimKinships(ped, allSimParents, pop = ped$id, n = n)
kValues <- kinshipMatricesToKValues(simKinships)
extractKValue(kValues, id1 = "A", id2 = "F", simulation = 1:10)

##  [1] "sim_1"  "sim_2"  "sim_3"  "sim_4"  "sim_5"  "sim_6"  "sim_7"  "sim_8" 
##  [9] "sim_9"  "sim_10"

counts <- countKinshipValues(kValues)
counts$kinshipIds[1:3]

## NULL

counts$kinshipValues[1:3]

## NULL

counts$kinshipCounts[1:3]

## NULL

stats_100 <- summarizeKinshipValues(counts)
nrow(stats_100[stats_100$sd > 0.0, ])

## [1] 94

kable(stats_100[stats_100$sd > 0.0, ], longtable = TRUE) %>%
  kable_styling(latex_options = c("striped", "repeat_header"),
                repeat_header_method = "replace",
                repeat_header_text = "\\textit{(continued)}")

	id_1	id_2	min	secondQuartile	mean	median	thirdQuartile	max	sd
5	A	E	0.00000	0.00000	0.0725000	0.000000	0.25000	0.25000	0.1140120
6	A	F	0.12500	0.12500	0.1612500	0.125000	0.25000	0.25000	0.0570060
7	A	G	0.12500	0.12500	0.1612500	0.125000	0.25000	0.25000	0.0570060
9	A	I	0.25000	0.25000	0.2825000	0.250000	0.37500	0.37500	0.0551055
10	A	J	0.00000	0.00000	0.0650000	0.000000	0.25000	0.25000	0.1102110
11	A	K	0.00000	0.00000	0.1000000	0.000000	0.25000	0.25000	0.1230915
12	A	L	0.12500	0.12500	0.1750000	0.125000	0.25000	0.25000	0.0615457
14	A	N	0.00000	0.00000	0.0950000	0.000000	0.25000	0.25000	0.1219579
21	B	E	0.00000	0.00000	0.1225000	0.000000	0.25000	0.25000	0.1256046
22	B	F	0.12500	0.12500	0.1862500	0.125000	0.25000	0.25000	0.0628023
23	B	G	0.12500	0.12500	0.1862500	0.125000	0.25000	0.25000	0.0628023
25	B	I	0.00000	0.00000	0.0512500	0.000000	0.12500	0.12500	0.0617889
26	B	J	0.00000	0.00000	0.1025000	0.000000	0.25000	0.25000	0.1235778
30	B	N	0.00000	0.00000	0.1325000	0.250000	0.25000	0.25000	0.1254034
36	C	E	0.00000	0.00000	0.0975000	0.125000	0.12500	0.25000	0.0862739
37	C	F	0.12500	0.12500	0.1737500	0.187500	0.18750	0.25000	0.0431369
38	C	G	0.12500	0.12500	0.1737500	0.187500	0.18750	0.25000	0.0431369
40	C	I	0.12500	0.12500	0.1668750	0.187500	0.18750	0.25000	0.0377465
41	C	J	0.00000	0.00000	0.0837500	0.125000	0.12500	0.25000	0.0754929
42	C	K	0.00000	0.00000	0.0500000	0.000000	0.12500	0.12500	0.0615457
43	C	L	0.25000	0.25000	0.2750000	0.250000	0.31250	0.31250	0.0307729
45	C	N	0.00000	0.00000	0.1137500	0.125000	0.12500	0.25000	0.0890023
50	D	E	0.00000	0.00000	0.0975000	0.125000	0.12500	0.25000	0.0862739
51	D	F	0.25000	0.25000	0.2987500	0.312500	0.31250	0.37500	0.0431369
52	D	G	0.25000	0.25000	0.2987500	0.312500	0.31250	0.37500	0.0431369
54	D	I	0.12500	0.12500	0.1668750	0.187500	0.18750	0.25000	0.0377465
55	D	J	0.00000	0.00000	0.0837500	0.125000	0.12500	0.25000	0.0754929
56	D	K	0.00000	0.00000	0.0500000	0.000000	0.12500	0.12500	0.0615457
57	D	L	0.12500	0.12500	0.1500000	0.125000	0.18750	0.18750	0.0307729
59	D	N	0.00000	0.00000	0.1137500	0.125000	0.12500	0.25000	0.0890023
64	E	F	0.25000	0.25000	0.2987500	0.312500	0.31250	0.37500	0.0431369
65	E	G	0.25000	0.25000	0.2987500	0.312500	0.31250	0.37500	0.0431369
66	E	H	0.00000	0.00000	0.0975000	0.125000	0.12500	0.25000	0.0862739
67	E	I	0.00000	0.00000	0.0643750	0.062500	0.12500	0.25000	0.0702039
68	E	J	0.00000	0.00000	0.0562500	0.000000	0.12500	0.25000	0.0782039
69	E	K	0.00000	0.00000	0.0312500	0.000000	0.06250	0.12500	0.0543993
70	E	L	0.00000	0.00000	0.0643750	0.062500	0.12500	0.18750	0.0578818
71	E	M	0.00000	0.00000	0.0362500	0.000000	0.12500	0.12500	0.0570060
72	E	N	0.00000	0.00000	0.0587500	0.000000	0.12500	0.25000	0.0742279
74	E	P	0.00000	0.00000	0.0181250	0.000000	0.06250	0.06250	0.0285030
75	E	Q	0.00000	0.00000	0.0362500	0.000000	0.12500	0.12500	0.0570060
76	F	F	0.50000	0.50000	0.5487500	0.562500	0.56250	0.62500	0.0431369
77	F	G	0.25000	0.25000	0.2987500	0.312500	0.31250	0.37500	0.0431369
78	F	H	0.12500	0.12500	0.1737500	0.187500	0.18750	0.25000	0.0431369
79	F	I	0.06250	0.06250	0.1156250	0.093750	0.12500	0.25000	0.0429490
80	F	J	0.00000	0.00000	0.0700000	0.062500	0.12500	0.25000	0.0623610
81	F	K	0.00000	0.00000	0.0406250	0.062500	0.06250	0.12500	0.0438581
82	F	L	0.06250	0.06250	0.1071875	0.093750	0.12500	0.18750	0.0341909
83	F	M	0.06250	0.06250	0.0806250	0.062500	0.12500	0.12500	0.0285030
84	F	N	0.00000	0.00000	0.0862500	0.062500	0.12500	0.25000	0.0681071
86	F	P	0.03125	0.03125	0.0403125	0.031250	0.06250	0.06250	0.0142515
87	F	Q	0.06250	0.06250	0.0806250	0.062500	0.12500	0.12500	0.0285030
88	G	G	0.50000	0.50000	0.5487500	0.562500	0.56250	0.62500	0.0431369
89	G	H	0.12500	0.12500	0.1737500	0.187500	0.18750	0.25000	0.0431369
90	G	I	0.06250	0.06250	0.1156250	0.093750	0.12500	0.25000	0.0429490
91	G	J	0.00000	0.00000	0.0700000	0.062500	0.12500	0.25000	0.0623610
92	G	K	0.00000	0.00000	0.0406250	0.062500	0.06250	0.12500	0.0438581
93	G	L	0.06250	0.06250	0.1071875	0.093750	0.12500	0.18750	0.0341909
94	G	M	0.06250	0.06250	0.0806250	0.062500	0.12500	0.12500	0.0285030
95	G	N	0.00000	0.00000	0.0862500	0.062500	0.12500	0.25000	0.0681071
97	G	P	0.03125	0.03125	0.0403125	0.031250	0.06250	0.06250	0.0142515
98	G	Q	0.06250	0.06250	0.0806250	0.062500	0.12500	0.12500	0.0285030
100	H	I	0.12500	0.12500	0.1668750	0.187500	0.18750	0.25000	0.0377465
101	H	J	0.00000	0.00000	0.0837500	0.125000	0.12500	0.25000	0.0754929
102	H	K	0.00000	0.00000	0.0500000	0.000000	0.12500	0.12500	0.0615457
103	H	L	0.12500	0.12500	0.1500000	0.125000	0.18750	0.18750	0.0307729
105	H	N	0.00000	0.00000	0.1137500	0.125000	0.12500	0.25000	0.0890023
109	I	I	0.50000	0.50000	0.5325000	0.500000	0.62500	0.62500	0.0551055
110	I	J	0.25000	0.25000	0.2825000	0.250000	0.37500	0.37500	0.0551055
111	I	K	0.00000	0.00000	0.0593750	0.000000	0.12500	0.18750	0.0655054
112	I	L	0.06250	0.06250	0.1131250	0.109375	0.12500	0.21875	0.0381520
113	I	M	0.12500	0.12500	0.1412500	0.125000	0.18750	0.18750	0.0275528
114	I	N	0.00000	0.00000	0.0756250	0.062500	0.12500	0.25000	0.0760527
116	I	P	0.06250	0.06250	0.0706250	0.062500	0.09375	0.09375	0.0137764
117	I	Q	0.12500	0.12500	0.1412500	0.125000	0.18750	0.18750	0.0275528
119	J	K	0.00000	0.00000	0.0187500	0.000000	0.00000	0.12500	0.0448588
120	J	L	0.00000	0.00000	0.0512500	0.062500	0.06250	0.18750	0.0464830
121	J	M	0.00000	0.00000	0.0325000	0.000000	0.12500	0.12500	0.0551055
122	J	N	0.00000	0.00000	0.0562500	0.000000	0.12500	0.25000	0.0673614
124	J	P	0.00000	0.00000	0.0162500	0.000000	0.06250	0.06250	0.0275528
125	J	Q	0.00000	0.00000	0.0325000	0.000000	0.12500	0.12500	0.0551055
127	K	L	0.25000	0.25000	0.2750000	0.250000	0.31250	0.31250	0.0307729
128	K	M	0.00000	0.00000	0.0500000	0.000000	0.12500	0.12500	0.0615457
129	K	N	0.00000	0.00000	0.0337500	0.000000	0.12500	0.12500	0.0557745
131	K	P	0.00000	0.00000	0.0250000	0.000000	0.06250	0.06250	0.0307729
132	K	Q	0.00000	0.00000	0.0500000	0.000000	0.12500	0.12500	0.0615457
133	L	L	0.50000	0.50000	0.5250000	0.500000	0.56250	0.56250	0.0307729
134	L	M	0.06250	0.06250	0.0875000	0.062500	0.12500	0.12500	0.0307729
135	L	N	0.00000	0.00000	0.0737500	0.062500	0.12500	0.18750	0.0585089
137	L	P	0.03125	0.03125	0.0437500	0.031250	0.06250	0.06250	0.0153864
138	L	Q	0.06250	0.06250	0.0875000	0.062500	0.12500	0.12500	0.0307729
140	M	N	0.00000	0.00000	0.0475000	0.000000	0.12500	0.12500	0.0609790
146	N	P	0.00000	0.00000	0.0237500	0.000000	0.06250	0.06250	0.0304895
147	N	Q	0.00000	0.00000	0.0475000	0.000000	0.12500	0.12500	0.0609790

A much larger simulation

set.seed(1)
n <- 1000
simKinships <- createSimKinships(ped, allSimParents, pop = ped$id, n = n)
kValues <- kinshipMatricesToKValues(simKinships)
extractKValue(kValues, id1 = "A", id2 = "F", simulation = 1:10)

##  [1] "sim_1"  "sim_2"  "sim_3"  "sim_4"  "sim_5"  "sim_6"  "sim_7"  "sim_8" 
##  [9] "sim_9"  "sim_10"

counts <- countKinshipValues(kValues)
counts$kinshipIds[1:3]

## NULL

counts$kinshipValues[1:3]

## NULL

counts$kinshipCounts[1:3]

## NULL

stats_1000 <- summarizeKinshipValues(counts)
nrow(stats_1000[stats_1000$sd > 0.0, ])

## [1] 94

kable(stats_1000[stats_1000$sd > 0.0, ], longtable = TRUE) %>%
  kable_styling(latex_options = c("striped", "repeat_header"),
                repeat_header_method = "replace",
                repeat_header_text = "\\textit{(continued)}")

	id_1	id_2	min	secondQuartile	mean	median	thirdQuartile	max	sd
5	A	E	0.00000	0.00000	0.0792500	0.00000	0.25000	0.25000	0.1163851
6	A	F	0.12500	0.12500	0.1646250	0.12500	0.25000	0.25000	0.0581925
7	A	G	0.12500	0.12500	0.1646250	0.12500	0.25000	0.25000	0.0581925
9	A	I	0.25000	0.25000	0.2886250	0.25000	0.37500	0.37500	0.0577890
10	A	J	0.00000	0.00000	0.0772500	0.00000	0.25000	0.25000	0.1155781
11	A	K	0.00000	0.00000	0.0910000	0.00000	0.25000	0.25000	0.1203473
12	A	L	0.12500	0.12500	0.1705000	0.12500	0.25000	0.25000	0.0601737
14	A	N	0.00000	0.00000	0.0840000	0.00000	0.25000	0.25000	0.1181438
21	B	E	0.00000	0.00000	0.1200000	0.00000	0.25000	0.25000	0.1249625
22	B	F	0.12500	0.12500	0.1850000	0.12500	0.25000	0.25000	0.0624812
23	B	G	0.12500	0.12500	0.1850000	0.12500	0.25000	0.25000	0.0624812
25	B	I	0.00000	0.00000	0.0558750	0.00000	0.12500	0.12500	0.0621790
26	B	J	0.00000	0.00000	0.1117500	0.00000	0.25000	0.25000	0.1243580
30	B	N	0.00000	0.00000	0.1207500	0.00000	0.25000	0.25000	0.1249902
36	C	E	0.00000	0.00000	0.0996250	0.12500	0.12500	0.25000	0.0859018
37	C	F	0.12500	0.12500	0.1748125	0.18750	0.18750	0.25000	0.0429509
38	C	G	0.12500	0.12500	0.1748125	0.18750	0.18750	0.25000	0.0429509
40	C	I	0.12500	0.12500	0.1722500	0.18750	0.18750	0.25000	0.0411218
41	C	J	0.00000	0.00000	0.0945000	0.12500	0.12500	0.25000	0.0822436
42	C	K	0.00000	0.00000	0.0455000	0.00000	0.12500	0.12500	0.0601737
43	C	L	0.25000	0.25000	0.2727500	0.25000	0.31250	0.31250	0.0300868
45	C	N	0.00000	0.00000	0.1023750	0.12500	0.12500	0.25000	0.0855778
50	D	E	0.00000	0.00000	0.0996250	0.12500	0.12500	0.25000	0.0859018
51	D	F	0.25000	0.25000	0.2998125	0.31250	0.31250	0.37500	0.0429509
52	D	G	0.25000	0.25000	0.2998125	0.31250	0.31250	0.37500	0.0429509
54	D	I	0.12500	0.12500	0.1722500	0.18750	0.18750	0.25000	0.0411218
55	D	J	0.00000	0.00000	0.0945000	0.12500	0.12500	0.25000	0.0822436
56	D	K	0.00000	0.00000	0.0455000	0.00000	0.12500	0.12500	0.0601737
57	D	L	0.12500	0.12500	0.1477500	0.12500	0.18750	0.18750	0.0300868
59	D	N	0.00000	0.00000	0.1023750	0.12500	0.12500	0.25000	0.0855778
64	E	F	0.25000	0.25000	0.2998125	0.31250	0.31250	0.37500	0.0429509
65	E	G	0.25000	0.25000	0.2998125	0.31250	0.31250	0.37500	0.0429509
66	E	H	0.00000	0.00000	0.0996250	0.12500	0.12500	0.25000	0.0859018
67	E	I	0.00000	0.00000	0.0670000	0.06250	0.12500	0.25000	0.0720825
68	E	J	0.00000	0.00000	0.0547500	0.00000	0.12500	0.25000	0.0740045
69	E	K	0.00000	0.00000	0.0278750	0.00000	0.00000	0.12500	0.0520583
70	E	L	0.00000	0.00000	0.0637500	0.06250	0.12500	0.18750	0.0527491
71	E	M	0.00000	0.00000	0.0396250	0.00000	0.12500	0.12500	0.0581925
72	E	N	0.00000	0.00000	0.0576250	0.00000	0.12500	0.25000	0.0744599
74	E	P	0.00000	0.00000	0.0198125	0.00000	0.06250	0.06250	0.0290963
75	E	Q	0.00000	0.00000	0.0396250	0.00000	0.12500	0.12500	0.0581925
76	F	F	0.50000	0.50000	0.5498125	0.56250	0.56250	0.62500	0.0429509
77	F	G	0.25000	0.25000	0.2998125	0.31250	0.31250	0.37500	0.0429509
78	F	H	0.12500	0.12500	0.1748125	0.18750	0.18750	0.25000	0.0429509
79	F	I	0.06250	0.06250	0.1196250	0.12500	0.15625	0.25000	0.0447920
80	F	J	0.00000	0.00000	0.0746250	0.06250	0.12500	0.25000	0.0651156
81	F	K	0.00000	0.00000	0.0366875	0.00000	0.06250	0.12500	0.0419673
82	F	L	0.06250	0.06250	0.1057500	0.09375	0.12500	0.18750	0.0305468
83	F	M	0.06250	0.06250	0.0823125	0.06250	0.12500	0.12500	0.0290963
84	F	N	0.00000	0.00000	0.0800000	0.06250	0.12500	0.25000	0.0662241
86	F	P	0.03125	0.03125	0.0411562	0.03125	0.06250	0.06250	0.0145481
87	F	Q	0.06250	0.06250	0.0823125	0.06250	0.12500	0.12500	0.0290963
88	G	G	0.50000	0.50000	0.5498125	0.56250	0.56250	0.62500	0.0429509
89	G	H	0.12500	0.12500	0.1748125	0.18750	0.18750	0.25000	0.0429509
90	G	I	0.06250	0.06250	0.1196250	0.12500	0.15625	0.25000	0.0447920
91	G	J	0.00000	0.00000	0.0746250	0.06250	0.12500	0.25000	0.0651156
92	G	K	0.00000	0.00000	0.0366875	0.00000	0.06250	0.12500	0.0419673
93	G	L	0.06250	0.06250	0.1057500	0.09375	0.12500	0.18750	0.0305468
94	G	M	0.06250	0.06250	0.0823125	0.06250	0.12500	0.12500	0.0290963
95	G	N	0.00000	0.00000	0.0800000	0.06250	0.12500	0.25000	0.0662241
97	G	P	0.03125	0.03125	0.0411562	0.03125	0.06250	0.06250	0.0145481
98	G	Q	0.06250	0.06250	0.0823125	0.06250	0.12500	0.12500	0.0290963
100	H	I	0.12500	0.12500	0.1722500	0.18750	0.18750	0.25000	0.0411218
101	H	J	0.00000	0.00000	0.0945000	0.12500	0.12500	0.25000	0.0822436
102	H	K	0.00000	0.00000	0.0455000	0.00000	0.12500	0.12500	0.0601737
103	H	L	0.12500	0.12500	0.1477500	0.12500	0.18750	0.18750	0.0300868
105	H	N	0.00000	0.00000	0.1023750	0.12500	0.12500	0.25000	0.0855778
109	I	I	0.50000	0.50000	0.5386250	0.50000	0.62500	0.62500	0.0577890
110	I	J	0.25000	0.25000	0.2886250	0.25000	0.37500	0.37500	0.0577890
111	I	K	0.00000	0.00000	0.0585000	0.00000	0.12500	0.18750	0.0684968
112	I	L	0.06250	0.06250	0.1153750	0.09375	0.12500	0.21875	0.0408748
113	I	M	0.12500	0.12500	0.1443125	0.12500	0.18750	0.18750	0.0288945
114	I	N	0.00000	0.00000	0.0693125	0.06250	0.12500	0.25000	0.0739647
116	I	P	0.06250	0.06250	0.0721562	0.06250	0.09375	0.09375	0.0144473
117	I	Q	0.12500	0.12500	0.1443125	0.12500	0.18750	0.18750	0.0288945
119	J	K	0.00000	0.00000	0.0260000	0.00000	0.00000	0.12500	0.0507600
120	J	L	0.00000	0.00000	0.0602500	0.06250	0.06250	0.18750	0.0518182
121	J	M	0.00000	0.00000	0.0386250	0.00000	0.12500	0.12500	0.0577890
122	J	N	0.00000	0.00000	0.0546250	0.00000	0.12500	0.25000	0.0731409
124	J	P	0.00000	0.00000	0.0193125	0.00000	0.06250	0.06250	0.0288945
125	J	Q	0.00000	0.00000	0.0386250	0.00000	0.12500	0.12500	0.0577890
127	K	L	0.25000	0.25000	0.2727500	0.25000	0.31250	0.31250	0.0300868
128	K	M	0.00000	0.00000	0.0455000	0.00000	0.12500	0.12500	0.0601737
129	K	N	0.00000	0.00000	0.0285000	0.00000	0.00000	0.12500	0.0524691
131	K	P	0.00000	0.00000	0.0227500	0.00000	0.06250	0.06250	0.0300868
132	K	Q	0.00000	0.00000	0.0455000	0.00000	0.12500	0.12500	0.0601737
133	L	L	0.50000	0.50000	0.5227500	0.50000	0.56250	0.56250	0.0300868
134	L	M	0.06250	0.06250	0.0852500	0.06250	0.12500	0.12500	0.0300868
135	L	N	0.00000	0.00000	0.0654375	0.06250	0.12500	0.18750	0.0533825
137	L	P	0.03125	0.03125	0.0426250	0.03125	0.06250	0.06250	0.0150434
138	L	Q	0.06250	0.06250	0.0852500	0.06250	0.12500	0.12500	0.0300868
140	M	N	0.00000	0.00000	0.0420000	0.00000	0.12500	0.12500	0.0590719
146	N	P	0.00000	0.00000	0.0210000	0.00000	0.06250	0.06250	0.0295360
147	N	Q	0.00000	0.00000	0.0420000	0.00000	0.12500	0.12500	0.0590719

Comparing the values and variation found for the various kinship values:

stats_short <- stats_10[stats_10$sd > 0.0, ]
stats_long <- stats_1000[stats_1000$sd > 0.0, ]

if (any(stats_short$id_1 != stats_long$id_1) ||
      any(stats_short$id_2 != stats_long$id_2))
  cat("At least one row represents a different animal pair")

comprison <- data.frame(
  id_1 = stats_short$id_1,
  id_2 = stats_short$id_2,
  meanKin_short = stats_short$mean,
  meanKin_long = stats_long$mean,
  meanKinDelta = abs(stats_short$mean - stats_long$mean),
  sdKin_short = stats_short$sd,
  sdKin_long = stats_long$sd,
  sdKinDelta = abs(stats_short$sd - stats_long$sd)
)

kable(comprison, longtable = TRUE,
      digits = c(0, 0, 4, 4, 4, 4, 4, 4),
      caption = stri_c("Comparision of estimated kinships between simulations ",
                       "of 10 (short) and 1000 (long)")) %>%
  kable_styling(latex_options = c("striped", "repeat_header"),
                repeat_header_method = "replace",
                repeat_header_text = "\\textit{(continued)}",
                font_size = 10)

Comparision of estimated kinships between simulations of 10 (short) and 1000 (long)
id_1	id_2	meanKin_short	meanKin_long	meanKinDelta	sdKin_short	sdKin_long	sdKinDelta
A	E	0.0750	0.0792	0.0043	0.1208	0.1164	0.0044
A	F	0.1625	0.1646	0.0021	0.0604	0.0582	0.0022
A	G	0.1625	0.1646	0.0021	0.0604	0.0582	0.0022
A	I	0.2625	0.2886	0.0261	0.0395	0.0578	0.0183
A	J	0.0250	0.0772	0.0522	0.0791	0.1156	0.0365
A	K	0.1250	0.0910	0.0340	0.1318	0.1203	0.0114
A	L	0.1875	0.1705	0.0170	0.0659	0.0602	0.0057
A	N	0.1000	0.0840	0.0160	0.1291	0.1181	0.0110
B	E	0.1500	0.1200	0.0300	0.1291	0.1250	0.0041
B	F	0.2000	0.1850	0.0150	0.0645	0.0625	0.0021
B	G	0.2000	0.1850	0.0150	0.0645	0.0625	0.0021
B	I	0.0625	0.0559	0.0066	0.0659	0.0622	0.0037
B	J	0.1250	0.1118	0.0132	0.1318	0.1244	0.0074
B	N	0.1000	0.1207	0.0207	0.1291	0.1250	0.0041
C	E	0.1125	0.0996	0.0129	0.1094	0.0859	0.0235
C	F	0.1812	0.1748	0.0064	0.0547	0.0430	0.0118
C	G	0.1812	0.1748	0.0064	0.0547	0.0430	0.0118
C	I	0.1625	0.1722	0.0097	0.0437	0.0411	0.0026
C	J	0.0750	0.0945	0.0195	0.0874	0.0822	0.0052
C	K	0.0625	0.0455	0.0170	0.0659	0.0602	0.0057
C	L	0.2812	0.2728	0.0085	0.0329	0.0301	0.0029
C	N	0.1000	0.1024	0.0024	0.0527	0.0856	0.0329
D	E	0.1125	0.0996	0.0129	0.1094	0.0859	0.0235
D	F	0.3062	0.2998	0.0064	0.0547	0.0430	0.0118
D	G	0.3062	0.2998	0.0064	0.0547	0.0430	0.0118
D	I	0.1625	0.1722	0.0097	0.0437	0.0411	0.0026
D	J	0.0750	0.0945	0.0195	0.0874	0.0822	0.0052
D	K	0.0625	0.0455	0.0170	0.0659	0.0602	0.0057
D	L	0.1562	0.1478	0.0085	0.0329	0.0301	0.0029
D	N	0.1000	0.1024	0.0024	0.0527	0.0856	0.0329
E	F	0.3062	0.2998	0.0064	0.0547	0.0430	0.0118
E	G	0.3062	0.2998	0.0064	0.0547	0.0430	0.0118
E	H	0.1125	0.0996	0.0129	0.1094	0.0859	0.0235
E	I	0.0688	0.0670	0.0018	0.0906	0.0721	0.0185
E	J	0.0625	0.0548	0.0078	0.0884	0.0740	0.0144
E	K	0.0875	0.0279	0.0596	0.0604	0.0521	0.0083
E	L	0.1000	0.0638	0.0363	0.0734	0.0527	0.0206
E	M	0.0375	0.0396	0.0021	0.0604	0.0582	0.0022
E	N	0.0500	0.0576	0.0076	0.0874	0.0745	0.0129
E	P	0.0187	0.0198	0.0011	0.0302	0.0291	0.0011
E	Q	0.0375	0.0396	0.0021	0.0604	0.0582	0.0022
F	F	0.5562	0.5498	0.0064	0.0547	0.0430	0.0118
F	G	0.3062	0.2998	0.0064	0.0547	0.0430	0.0118
F	H	0.1812	0.1748	0.0064	0.0547	0.0430	0.0118
F	I	0.1156	0.1196	0.0040	0.0608	0.0448	0.0160
F	J	0.0688	0.0746	0.0059	0.0804	0.0651	0.0153
F	K	0.0750	0.0367	0.0383	0.0395	0.0420	0.0024
F	L	0.1281	0.1057	0.0224	0.0453	0.0305	0.0147
F	M	0.0813	0.0823	0.0011	0.0302	0.0291	0.0011
F	N	0.0750	0.0800	0.0050	0.0574	0.0662	0.0088
F	P	0.0406	0.0412	0.0005	0.0151	0.0145	0.0005
F	Q	0.0813	0.0823	0.0011	0.0302	0.0291	0.0011
G	G	0.5562	0.5498	0.0064	0.0547	0.0430	0.0118
G	H	0.1812	0.1748	0.0064	0.0547	0.0430	0.0118
G	I	0.1156	0.1196	0.0040	0.0608	0.0448	0.0160
G	J	0.0688	0.0746	0.0059	0.0804	0.0651	0.0153
G	K	0.0750	0.0367	0.0383	0.0395	0.0420	0.0024
G	L	0.1281	0.1057	0.0224	0.0453	0.0305	0.0147
G	M	0.0813	0.0823	0.0011	0.0302	0.0291	0.0011
G	N	0.0750	0.0800	0.0050	0.0574	0.0662	0.0088
G	P	0.0406	0.0412	0.0005	0.0151	0.0145	0.0005
G	Q	0.0813	0.0823	0.0011	0.0302	0.0291	0.0011
H	I	0.1625	0.1722	0.0097	0.0437	0.0411	0.0026
H	J	0.0750	0.0945	0.0195	0.0874	0.0822	0.0052
H	K	0.0625	0.0455	0.0170	0.0659	0.0602	0.0057
H	L	0.1562	0.1478	0.0085	0.0329	0.0301	0.0029
H	N	0.1000	0.1024	0.0024	0.0527	0.0856	0.0329
I	I	0.5125	0.5386	0.0261	0.0395	0.0578	0.0183
I	J	0.2625	0.2886	0.0261	0.0395	0.0578	0.0183
I	K	0.0750	0.0585	0.0165	0.0710	0.0685	0.0025
I	L	0.1187	0.1154	0.0034	0.0506	0.0409	0.0097
I	M	0.1312	0.1443	0.0131	0.0198	0.0289	0.0091
I	N	0.0688	0.0693	0.0006	0.0688	0.0740	0.0052
I	P	0.0656	0.0722	0.0065	0.0099	0.0144	0.0046
I	Q	0.1312	0.1443	0.0131	0.0198	0.0289	0.0091
J	K	0.0250	0.0260	0.0010	0.0527	0.0508	0.0019
J	L	0.0500	0.0602	0.0102	0.0645	0.0518	0.0127
J	M	0.0125	0.0386	0.0261	0.0395	0.0578	0.0183
J	N	0.0375	0.0546	0.0171	0.0604	0.0731	0.0128
J	P	0.0063	0.0193	0.0131	0.0198	0.0289	0.0091
J	Q	0.0125	0.0386	0.0261	0.0395	0.0578	0.0183
K	L	0.2812	0.2728	0.0085	0.0329	0.0301	0.0029
K	M	0.0625	0.0455	0.0170	0.0659	0.0602	0.0057
K	N	0.0500	0.0285	0.0215	0.0645	0.0525	0.0121
K	P	0.0312	0.0227	0.0085	0.0329	0.0301	0.0029
K	Q	0.0625	0.0455	0.0170	0.0659	0.0602	0.0057
L	L	0.5312	0.5228	0.0085	0.0329	0.0301	0.0029
L	M	0.0938	0.0853	0.0085	0.0329	0.0301	0.0029
L	N	0.0750	0.0654	0.0096	0.0493	0.0534	0.0041
L	P	0.0469	0.0426	0.0042	0.0165	0.0150	0.0014
L	Q	0.0938	0.0853	0.0085	0.0329	0.0301	0.0029
M	N	0.0500	0.0420	0.0080	0.0645	0.0591	0.0055
N	P	0.0250	0.0210	0.0040	0.0323	0.0295	0.0027
N	Q	0.0500	0.0420	0.0080	0.0645	0.0591	0.0055

stats_short <- stats_100[stats_100$sd > 0.0, ]
stats_long <- stats_1000[stats_1000$sd > 0.0, ]

if (any(stats_short$id_1 != stats_long$id_1) ||
      any(stats_short$id_2 != stats_long$id_2))
  cat("At least one row represents a different animal pair")

comprison <- data.frame(
  id_1 = stats_short$id_1,
  id_2 = stats_short$id_2,
  meanKin_short = stats_short$mean,
  meanKin_long = stats_long$mean,
  meanKinDelta = abs(stats_short$mean - stats_long$mean),
  sdKin_short = stats_short$sd,
  sdKin_long = stats_long$sd,
  sdKinDelta = abs(stats_short$sd - stats_long$sd)
)

kable(comprison, longtable = TRUE,
      digits = c(0, 0, 4, 4, 4, 4, 4, 4),
      caption = stri_c("Comparision of estimated kinships between simulations ",
                       "of 100 (short) and 1000 (long)")) %>%
  kable_styling(latex_options = c("striped", "repeat_header"),
                repeat_header_method = "replace",
                repeat_header_text = "\\textit{(continued)}",
                font_size = 10)

Comparision of estimated kinships between simulations of 100 (short) and 1000 (long)
id_1	id_2	meanKin_short	meanKin_long	meanKinDelta	sdKin_short	sdKin_long	sdKinDelta
A	E	0.0725	0.0792	0.0068	0.1140	0.1164	0.0024
A	F	0.1612	0.1646	0.0034	0.0570	0.0582	0.0012
A	G	0.1612	0.1646	0.0034	0.0570	0.0582	0.0012
A	I	0.2825	0.2886	0.0061	0.0551	0.0578	0.0027
A	J	0.0650	0.0772	0.0122	0.1102	0.1156	0.0054
A	K	0.1000	0.0910	0.0090	0.1231	0.1203	0.0027
A	L	0.1750	0.1705	0.0045	0.0615	0.0602	0.0014
A	N	0.0950	0.0840	0.0110	0.1220	0.1181	0.0038
B	E	0.1225	0.1200	0.0025	0.1256	0.1250	0.0006
B	F	0.1862	0.1850	0.0013	0.0628	0.0625	0.0003
B	G	0.1862	0.1850	0.0013	0.0628	0.0625	0.0003
B	I	0.0512	0.0559	0.0046	0.0618	0.0622	0.0004
B	J	0.1025	0.1118	0.0093	0.1236	0.1244	0.0008
B	N	0.1325	0.1207	0.0118	0.1254	0.1250	0.0004
C	E	0.0975	0.0996	0.0021	0.0863	0.0859	0.0004
C	F	0.1737	0.1748	0.0011	0.0431	0.0430	0.0002
C	G	0.1737	0.1748	0.0011	0.0431	0.0430	0.0002
C	I	0.1669	0.1722	0.0054	0.0377	0.0411	0.0034
C	J	0.0838	0.0945	0.0107	0.0755	0.0822	0.0068
C	K	0.0500	0.0455	0.0045	0.0615	0.0602	0.0014
C	L	0.2750	0.2728	0.0023	0.0308	0.0301	0.0007
C	N	0.1138	0.1024	0.0114	0.0890	0.0856	0.0034
D	E	0.0975	0.0996	0.0021	0.0863	0.0859	0.0004
D	F	0.2988	0.2998	0.0011	0.0431	0.0430	0.0002
D	G	0.2988	0.2998	0.0011	0.0431	0.0430	0.0002
D	I	0.1669	0.1722	0.0054	0.0377	0.0411	0.0034
D	J	0.0838	0.0945	0.0107	0.0755	0.0822	0.0068
D	K	0.0500	0.0455	0.0045	0.0615	0.0602	0.0014
D	L	0.1500	0.1478	0.0023	0.0308	0.0301	0.0007
D	N	0.1138	0.1024	0.0114	0.0890	0.0856	0.0034
E	F	0.2988	0.2998	0.0011	0.0431	0.0430	0.0002
E	G	0.2988	0.2998	0.0011	0.0431	0.0430	0.0002
E	H	0.0975	0.0996	0.0021	0.0863	0.0859	0.0004
E	I	0.0644	0.0670	0.0026	0.0702	0.0721	0.0019
E	J	0.0562	0.0548	0.0015	0.0782	0.0740	0.0042
E	K	0.0312	0.0279	0.0034	0.0544	0.0521	0.0023
E	L	0.0644	0.0638	0.0006	0.0579	0.0527	0.0051
E	M	0.0362	0.0396	0.0034	0.0570	0.0582	0.0012
E	N	0.0587	0.0576	0.0011	0.0742	0.0745	0.0002
E	P	0.0181	0.0198	0.0017	0.0285	0.0291	0.0006
E	Q	0.0362	0.0396	0.0034	0.0570	0.0582	0.0012
F	F	0.5488	0.5498	0.0011	0.0431	0.0430	0.0002
F	G	0.2988	0.2998	0.0011	0.0431	0.0430	0.0002
F	H	0.1737	0.1748	0.0011	0.0431	0.0430	0.0002
F	I	0.1156	0.1196	0.0040	0.0429	0.0448	0.0018
F	J	0.0700	0.0746	0.0046	0.0624	0.0651	0.0028
F	K	0.0406	0.0367	0.0039	0.0439	0.0420	0.0019
F	L	0.1072	0.1057	0.0014	0.0342	0.0305	0.0036
F	M	0.0806	0.0823	0.0017	0.0285	0.0291	0.0006
F	N	0.0862	0.0800	0.0062	0.0681	0.0662	0.0019
F	P	0.0403	0.0412	0.0008	0.0143	0.0145	0.0003
F	Q	0.0806	0.0823	0.0017	0.0285	0.0291	0.0006
G	G	0.5488	0.5498	0.0011	0.0431	0.0430	0.0002
G	H	0.1737	0.1748	0.0011	0.0431	0.0430	0.0002
G	I	0.1156	0.1196	0.0040	0.0429	0.0448	0.0018
G	J	0.0700	0.0746	0.0046	0.0624	0.0651	0.0028
G	K	0.0406	0.0367	0.0039	0.0439	0.0420	0.0019
G	L	0.1072	0.1057	0.0014	0.0342	0.0305	0.0036
G	M	0.0806	0.0823	0.0017	0.0285	0.0291	0.0006
G	N	0.0862	0.0800	0.0062	0.0681	0.0662	0.0019
G	P	0.0403	0.0412	0.0008	0.0143	0.0145	0.0003
G	Q	0.0806	0.0823	0.0017	0.0285	0.0291	0.0006
H	I	0.1669	0.1722	0.0054	0.0377	0.0411	0.0034
H	J	0.0838	0.0945	0.0107	0.0755	0.0822	0.0068
H	K	0.0500	0.0455	0.0045	0.0615	0.0602	0.0014
H	L	0.1500	0.1478	0.0023	0.0308	0.0301	0.0007
H	N	0.1138	0.1024	0.0114	0.0890	0.0856	0.0034
I	I	0.5325	0.5386	0.0061	0.0551	0.0578	0.0027
I	J	0.2825	0.2886	0.0061	0.0551	0.0578	0.0027
I	K	0.0594	0.0585	0.0009	0.0655	0.0685	0.0030
I	L	0.1131	0.1154	0.0023	0.0382	0.0409	0.0027
I	M	0.1412	0.1443	0.0031	0.0276	0.0289	0.0013
I	N	0.0756	0.0693	0.0063	0.0761	0.0740	0.0021
I	P	0.0706	0.0722	0.0015	0.0138	0.0144	0.0007
I	Q	0.1412	0.1443	0.0031	0.0276	0.0289	0.0013
J	K	0.0187	0.0260	0.0072	0.0449	0.0508	0.0059
J	L	0.0512	0.0602	0.0090	0.0465	0.0518	0.0053
J	M	0.0325	0.0386	0.0061	0.0551	0.0578	0.0027
J	N	0.0562	0.0546	0.0016	0.0674	0.0731	0.0058
J	P	0.0163	0.0193	0.0031	0.0276	0.0289	0.0013
J	Q	0.0325	0.0386	0.0061	0.0551	0.0578	0.0027
K	L	0.2750	0.2728	0.0023	0.0308	0.0301	0.0007
K	M	0.0500	0.0455	0.0045	0.0615	0.0602	0.0014
K	N	0.0338	0.0285	0.0053	0.0558	0.0525	0.0033
K	P	0.0250	0.0227	0.0023	0.0308	0.0301	0.0007
K	Q	0.0500	0.0455	0.0045	0.0615	0.0602	0.0014
L	L	0.5250	0.5228	0.0022	0.0308	0.0301	0.0007
L	M	0.0875	0.0853	0.0022	0.0308	0.0301	0.0007
L	N	0.0737	0.0654	0.0083	0.0585	0.0534	0.0051
L	P	0.0437	0.0426	0.0011	0.0154	0.0150	0.0003
L	Q	0.0875	0.0853	0.0022	0.0308	0.0301	0.0007
M	N	0.0475	0.0420	0.0055	0.0610	0.0591	0.0019
N	P	0.0238	0.0210	0.0027	0.0305	0.0295	0.0010
N	Q	0.0475	0.0420	0.0055	0.0610	0.0591	0.0019

nprcgenekeepr: an R Package for the Genetic Management of Colonies

R. Mark Sharp, Ph.D.

8/29/2021

Introduction

Anticipation of further uses of this kinship estimation method

Identification of potential parents

Creation of example pedigree²

Small Example

Quick Example of Simulated Kinships with Partial Parentage

nprcgenekeepr: an R Package for the Genetic Management of Colonies

R. Mark Sharp, Ph.D.

8/29/2021

Introduction

Anticipation of further uses of this kinship estimation method

Identification of potential parents

Creation of example pedigree2

Small Example

Creation of example pedigree²